Computing has been evolving by picking concepts from other areas and adapting those concepts. Neural networks, for example, come from observing the human brain; the application of design patterns and well-known solutions is common in architecture; did you ever feel like a doctor asking the patient what’s happening while debugging? A genetic algorithm originate from the genetics field, and a lot of terms are shared.
A bit of genetics
Let’s start having a look at Biology. An overly simplistic vision of the natural selection and evolution implies multiple individuals, each one with different characteristics, choosing whoever is the fittest over several generations.
We’ll use some of these concepts around genetics and apply them to computing.
- Gene: the minimum information we’ll have to deal with.
- Chromosome / genotype: the list of genes conforming an individual
- Population / phenotype: a list of chromosomes.
We’ll also need to define several operators:
- Mutation: just change one or more genes in a chromosome from its original state.
- Crossover: combine 2 chromosomes to generate a new one.
- Selection: choose the fittest chromosome
Mixing genetics with computing
Mutations
The mutation of a gene happens accordingly to a determined probability, usually user-defined, but it might be part of the problem’s definition: maybe we want to have up to 5 mutations in the chromosome, maybe 10, or maybe just 1. Note that the gene where the mutation happens should be completely random.
The mutation will change the value contained in the gene. This change can set a random value between boundaries, with a uniform or gaussian distribution depending on the problem’s definition. It can also swap values with another randomly chosen gene of the same chromosome.
Setting up these mutations is part of the problem definition: what mutations can happen and with what probability.
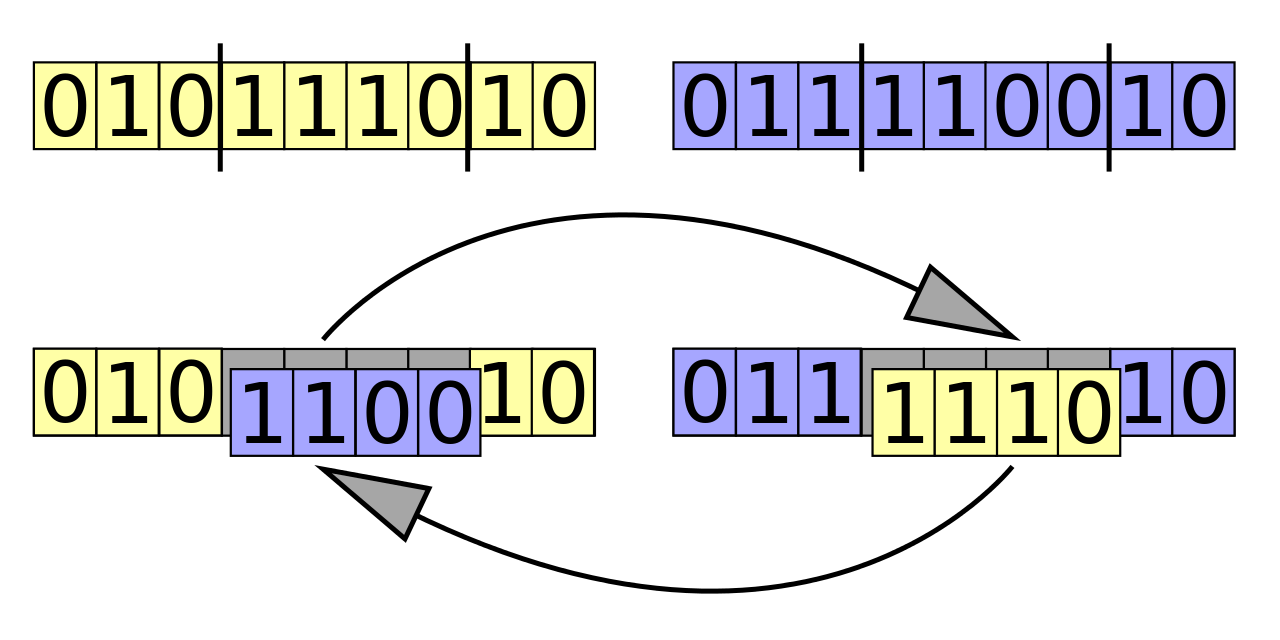
Crossovers
Similar to what happens to the mutation, the crossover has its own operations that can be setup or not depending on the particular problem. The common crossover operation consist on choosing a “crossover point” (or multiple points) and swap the parts of the chromosomes to generate a new one.
For example, if we have chromosomes A and B, we can split those into A1,A2,A3 and B1,B2,B3 and then generate A1,B2,A3 and B1,A2,B3. The crossover point must cut the pair of chromosomes in the same place.
Note that this crossover method might not be applicable to all problems because it can generate invalid solutions to the problem we want to solve.
Selections
Finally, the selection process selects the (usually) best group of chromosomes. In order to do so, the user needs to define a fitness function, which depends on the particular problem, in order to evaluate how fit the chromosome is. A fitter chromosome will have a higher value than another.
Once all chromosomes have their fitness evaluated, we’ll have to choose the “best” ones. Again, there are several methods to do this. The simplest method is to choose the ones with the higher fitness value, which are expected to be the ones closer to the solution of our problem.
How a genetic algorithm works
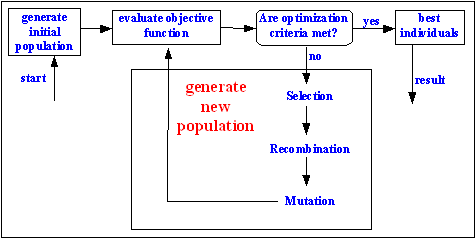
The overall process is:
- Apply the mutations to all the chromosomes. As said, some chromosomes might not mutate while others might have several mutations
- Generate new chromosomes via crossover. This step might be skipped if it doesn’t make sense for the problem.
- Apply the fitness function and select the best chromosomes. The chromosomes that aren’t selected will be discarded.
- Go to step 1.
This is an iterative process, and it will continue until some conditions are met. Usually, a mix of the following conditions are required to finish the iterative process (the conditions are also part of the problem definition)
- The highest fitness value hasn’t changed in the last X iterations. This means that you’ve found, very likely, the best solution.
- The highest fitness value is inside an acceptable threshold. The solution found might not be the best one, but it’s good enough.
- Finish after X iterations. This is usually set as a safety net in order to avoid an possible infinite loop.
Modeling a problem for a genetic algorithm
We want to send a list of 1000 files whose size varies between 0.5MB and 10MB. This are the restrictions:
- The size of the package must be less than 30MB (let’s assume you can’t upload files bigger than that).
- We want to minimize the number of packages we want to upload, so the package size must be as near as possible to 30MB but it can’t be bigger.
- We can accept a threshold of 500KB, so if we find a list of files of 29.5MB we’ll accept that package and stop looking for a better one.
- In order to simplify the problem, we’ll find an acceptable package of up to 30MB, remove those files from the list of files and repeat. We just need to find the first package of files.
In order to model the problem, each file will be a gene, the whole list of files will be a chromosome, and the population will be the possible variations of the list of files. We can start with a population size of 40 possible solutions randomly generated.
We need to define the list of operators we’re going to use.
- Mutations: we’ll focus on swapping genes, so any operator that perform this swapping is enough.
- Crossovers: we can apply a greedy crossover, which seems applicable for our case, or maybe a “do-nothing” crossover.
- Fitness function, we’ll check the first files in the list adding their sizes until we are at the closest point to the 30MB without going over it; the closest the better.
After modeling the problem, we can setup a genetic algorithm library with this information. Most of the libraries should have enough operators by default, so as said, it should be just configure the library properly and run it; usually you shouldn’t need to implement custom operators.
Last words

As you’ve seen, the overall process of a genetic algorithm is quite simple and easy to understand, but we haven’t look into the abyss, not even the surface.
The operators used by the algorithm usually determine the performance. Using a wrong operator could slow down the performance or even could fail the algorithm. It also could degenerate to a completely random search instead of improving each time.
You should use a library because it hides all the complexity that the operators can have. We’ve briefly mention the “greedy crossover”, which is used to solve the “traveling salesman problem”. There are studies aiming to improve the performance, and the topic is quite complex to follow.
Did you ever thought about using a genetic algorithm to solve a problem?




